|
Erklärung der Grundlangen: von: Ansgar Schiffler
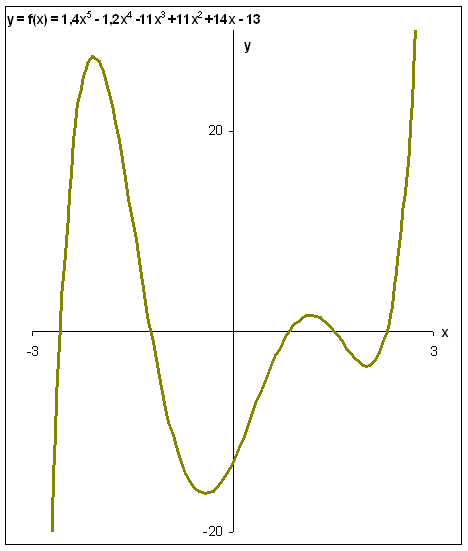
Das Bild zeigt den Graphen einer Funktion fünften Grades.
Die allgemeine Funktionsgleichung lautet:
y = f(x) = a·x5 + b·x4 + c·x3 + d·x2 +e·x + f
Die Gleichung des oben dargestellten Graphen lautet:
y = f(x) = 1,4·x5 -1,2·x4 - 11x3 + 11x2 + 14x -13
Der höchste in der Gleichung vorkommende Exponent ist 5, also ungerade.
Wenn der höchste Exponent ungerade ist, kommt der Graph aus der einen Richtung und verschwindet in die andere Richtung.
Für a > 0 kommt der Graph von links unten und verschwindet nach rechts oben. Dies ist in obigem Beispiel der Fall, denn es ist a = 1,4 > 0.
Für a < 0 kommt der Graph von links oben und verschwindet nach rechts unten.
Wie sieht es aus, wenn der höchste Exponent gerade ist, zum Beispiel bei einer Funktion vierten Grades mit der Gleichung y = f(x) = a·x4 + b·x3 + c·x2 + d·x +e ?
Wenn der höchste Exponent gerade ist, kommt der Graph aus der einen Richtung und verschwindet in die gleiche Richtung.
Für a > 0 kommt der Graph von links oben und verschwindet nach rechts oben.
Für a < 0 kommt der Graph von links unten und verschwindet nach rechts unten.
Der konstante Summand, also der Term, der kein x enthält, steht in der Regel ganz am Ende der Funktionsgleichung. In obigem Beispiel ist f = -13. Dies ist der y-Achsenabschnitt und gibt an, wo der Graph die y-Achse schneidet. Im obigem Beispiel schneidet der Graph die y-Achse also unterhalb der x-Achse.
Der Koeffizient, der vor dem x steht (in obigem Beispiel e = 14), gibt uns die Steigung des Graphen im y-Achsenabschnitt an. In obigem Beispiel ist die Steigung des Graphen im y-Achsenabschnitt also positiv.
Der Koeffizient, der vor dem x² steht (in obigem Beispiel d = 11), gibt uns die das Krümmungsverhalten des Graphen im y-Achsenabschnitt an. In obigem Beispiel ist d = 11> 0, die Steigung im y-Achsenabschnitt ist also zunehmend, der y-Achsenabschnitt befindet sich somit in einer Linkskurve. Für d < 0 befände sich der y-Achsenabschnitt in einer Rechtskurve (abnehmende Steigung).
Zusammenfassung:
Wenn wir also nur den Graphen sehen und wissen, dass die Funktionsgleichung y = f(x) = a·x5 + b·x4 + c·x3 + d·x2 +e·x + f lautet, können wir folgende Aussagen über die Koeffizienten treffen: a > 0, weil der Graph von links unten kommt und nach rechts oben verschwindet. f < 0, weil der Graph die y-Achse unterhalb der x-Achse schneidet. e > 0, weil die Steigung des Graphen im y-Achsenabschnitt positiv ist. d > 0, weil sich der y-Achsenabschnitt in einer Linkskurve befindet.
Aussagen über die übrigen Koeffizienten b und c sind auch möglich. Hierfür ist aber deutlich größerer Aufwand erforderlich.
Hinweis:
Anhand des Graphen ist auch erkennbar, dass die Funktionsgleichung mindestens fünften Grades sein muss.
Der Graph hat fünf Nullstellen daher muss die Funktionsgleichung mindestens den Grad fünf haben.
Der Graph weist vier Extremstellen auf (zwei lokale Tiefpunkte und zwei lokale Hochpunkte). Der Grad einer Funktionsgleichung muss mindestens um 1 höher sein als die Anzahl der Extremstellen, also bei diesem Graph mindestens fünf betragen.
Der Graph weist drei Wendepunkte auf (Übergang von Links- zu Rechtskurve oder umgekehrt). Der Grad einer Funktionsgleichung muss mindestens um 2 höher sein als die Anzahl der Wendepunkte, also bei diesem Graph mindestens fünf betragen.
Eine Funktion n-ten Grades (n > 2) hat höchstens n Nullstellen, höchstens n -1 Extremstellen und höchstens n - 2 Wendepunkte.
|