Übungsaufgaben zu Exponentialgleichungen

Übungsaufgaben zu Exponentialgleichungen

von: Ansgar Schiffler

2. Es sollen die Anzahl Bakterien zweier Bakterienkulturen miteinander verglichen werden.

Für beide Bakterienkulturen lässt sich die Anzahl der Bakterien in Abhängigkeit von der Zeit mit einer Funktion darstellen:

Kultur A: y = f_A(t) = C·e ^kt Kultur B: y = f_B(t) = D·e ^nt , wobei t die Zeit in Sekunden ist und y die Anzahl der Bakterien.

Zum Zeitpunkt t = 0 hat Kultur A 100.000 Bakterien und Kultur B 125.000 Bakterien. Nach drei Stunden hat Kultur A 117.000 Bakterien und Kultur B 132.000 Bakterien.

a.) Nach welcher Zeit werden beide Kulturen die gleiche Anzahl Bakterien haben? Wie groß sind die beiden Kulturen dann?

b.) Nach welcher Zeit wird Kultur A um ein Fünftel, also um 20%, größer sein als Kultur B? Wie groß sind die beiden Kulturen dann?

Musterlösung

2. gegeben: Kultur A: y = f_A(t) = C·e ^kt Kultur B: y = f_B(t) = D·e ^nt

Zum Zeitpunkt t = 0 besteht Kultur A aus 100.000 Bakterien. Wenn wir in die Gleichung für f_A(t) t = 0 einsetzen, müssen wir das Ergebnis 100.000 erhalten. Hieraus ergibt sich die folgende Gleichung:

100.000 = f_A(0) = C·e ^k·0

Es ist e ^k·0 = e ⁰ = 1 Wir erhalten somit C = 100.000

Genauso erhalten wir für Kultur B das Ergebnis D = 125.000

Zum Zeitpunkt t = 10.800 besteht Kultur A aus 117.000 Bakterien. Wenn wir in die Gleichung für f_A(t) t = 10.800 einsetzen, müssen wir das Ergebnis 117.000 erhalten. Hieraus ergibt sich die folgende Gleichung:

Hinweis: t wird in Sekunden angegeben. Drei Stunden entsprechen 10.800 Sekunden.

117.000 = f_A(10.800) = 100.000·e ^k·10.800

Um k zu bestimmen, lösen wir also diese Gleichung nach k auf:

117.000 = 100.000 · e ^k·10.800 | : 100.000

1,17 = e ^k·10.800 | ln

k · 10.800 = ln 1,17 | : 10.800

k = ln 1,17 / 10.800 ≈ 1,4537 · 10^-5

Genau auf die gleiche Art bestimmen Sie nun n.

Ansatz: 132.000 = 125.000 · e ^n·10.800

Ergebnis: n = ln (132/125) / 10.800 ≈ 5,0452 · 10^-6

Nun sind beiden Funktionsgleichungen ermittelt:

Kultur A: y = f_A(t) = 100.000·e ^k·t mit k ≈ 1,4537 · 10^-5

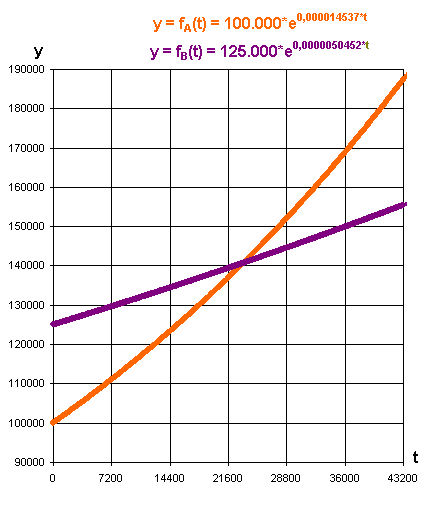
Kultur B: y = f_B(t) = 125.000·e ^n·t mit n ≈ 5,0452 · 10^-6

Die Graphen der beiden Funktionen:

Beachten Sie, dass die t-Achse in 2h-Abschnitte unterteilt ist: Von 0 bis 12 h (halber Tag)

Der Graph von f_B(t) sieht auf den ersten Blick wie eine Gerade aus. Dies ist jedoch nicht der Fall.

Jetzt können wir Aufgabe a lösen.

a.) Nach welcher Zeit werden beide Kulturen die gleiche Anzahl Bakterien haben? Wie groß sind die beiden Kulturen dann?

Es werden die beiden Funktionsgleichungen gleichgesetzt. Diese Gleichung lösen wir dann nach t auf.

Ansatz: f_A(t) = f_B(t)

C·e ^k·t = D·e ^n·t | : C | : e ^k·t

e ^k·t/ e ^n·t = D / C | T Hinweis: T steht für 'Termumformung'

e ^{k·t – n·t} = D / C | ln

Hinweis: Zwei Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert (und die Basis beibehält)

k·t – n·t = ln (D / C) | T

t · (k – n) = ln (D / C) | : (k – n)

t = ln (D / C) / (k – n)

Wir setzen jetzt die uns bekannten Werte für C, D, k und n ein:

t = ln(125.000/100.000) / (1,4537 · 10^-5 – 5,0452 · 10^-6) ≈ 23.508

Nach ca. 23.508 Sekunden, also nach 6h 31 Min. 48 Sek. sind beide Kulturen gleich groß.

Wir bestimmen die Größe der Kulturen, indem wir t = 23.508 in beide Funktionsgleichungen einsetzen:

y = f_A(t) = 100.000 · e ^{0,000014537 · 23.508} ≈ 140.740

y = f_B(t) = 125.000 · e ^{0,0000050452 · 23.508} ≈ 140.740

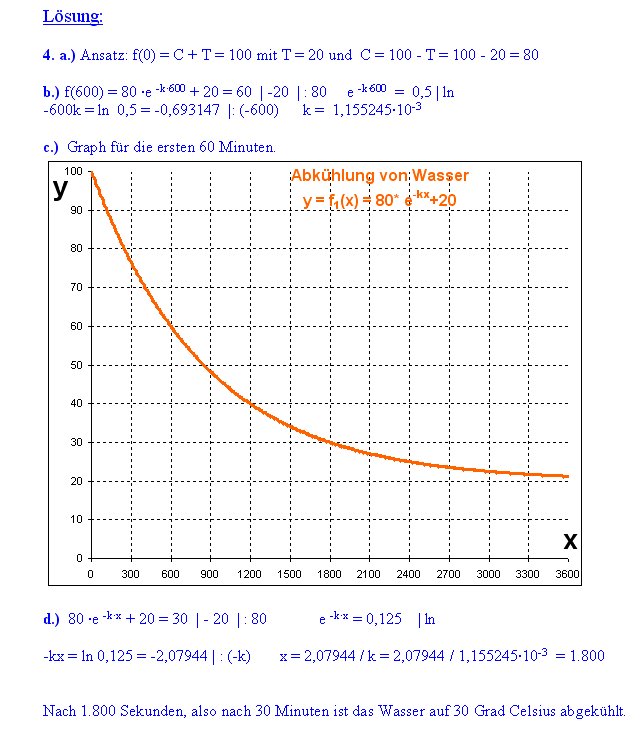
Beide Kulturen bestehen dann aus ca. 140.740 Bakterien.

b.) Nach welcher Zeit wird Kultur A um ein Fünftel, also um 20%, größer sein als Kultur B? Wie groß sind die beiden Kulturen dann?

Zur Erinnerung. Das war der Ansatz für Aufgabe a (beide Kulturen sind gleich groß):

f_A(t) = f_B(t)

Nun ist gefragt, zu welchem Zeitpunkt Kultur A um 20% größer ist als Kultur B.

Wir müssen also zu der Größe der Kultur B 20% hinzuaddieren um auf die Größe der Kultur A zu kommen. Eine Addition von 20% entspricht einer Multiplikation mit dem Faktor 1,2. Beispiel: Wenn Sie zu 100 20% hinzuaddieren, erhalten Sie 120. Wenn Sie 100 mit dem Faktor 1,2 multiplizieren, erhalten Sie ebenfalls 120.

Dies ist also der Ansatz:

f_A(t) = 1,2 · f_B(t)

C·e ^k·t = 1,2 · D·e ^n·t

Diese Gleichung lösen wir nun nach t auf und erhalten folgendes Ergbnis (die Rechenschritte sind mit Aufgabe a identisch):

t = ln (1,2 · D / C) / (k – n)

Wir setzen jetzt die uns bekannten Werte für C, D, k und n ein:

t = ln(1,5) / (1,4537 · 10^-5 – 5,0452 · 10^-6) ≈ 42.716

Nach ca. 42.716 Sekunden, also nach 11 h 51 Min. 56 Sek. ist Kultur A um 20% größer als Kultur B.

Wir bestimmen die Größe der Kulturen, indem wir t = 42.716 in beide Funktionsgleichungen einsetzen:

y = f_A(t) = 100.000 · e ^{0,000014537
· 42.716} ≈ 186.074

y = f_B(t) = 125.000 · e ^{0,0000050452 · 42.716} ≈ 155.062

Kultur A besteht dann aus ca. 186.074 Bakterien und Kultur B besteht dann aus ca. 155.062 Bakterien.

Hinweis: Als Probe können Sie zu 155.062 20% hinzuaddieren. Sie erhalten dann den gerundeten Wert 186.074.

zurück zu 'Exponentialgleichungen'

3. Eine Bakterienkultur besteht nach zwei Stunden aus 100.000 Bakterien. Sechs Stunden später ist die Anzahl der Bakterien um 22.000 angestiegen. Die Anzahl der Bakterien in Abhängigkeit von der Zeit lässt sich so mit einer Funktion darstellen:

y = f(t) = C·e ^kt , wobei t die Zeit in Sekunden ist und y die Anzahl der Bakterien.

a.) Bestimmen Sie C und k.

b.) Wie viele Bakterien wird es nach einem Tag geben?

c.) Nach welcher Zeit wird es 200.000 Bakterien geben? Geben Sie das Ergebnis auf eine Sekunde gerundet an.

3 a.)

y = f(7200) = 100.000 I C·e ^7200k = 100.000

y = f(28.800) = 122.000 II C·e ^28.800k = 122.000

Wir erhalten also ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten. Wir lösen dieses Gleichungssystem mitHilfe des Einsetzungs- verfahrens.

1. Schritt: Gleichung II nach C aufösen.

C·e ^28.800k = 122.000 | : e ^28.800k

2. Schritt: C in Gleichung I einsetzen und diese Gleichung nach k auflösen.

C = 122.000 ·e ^-28.800k in I einsetzen:

122.000 ·e ^-28.800k·e ^7.200k = 100.000 | : 100.000

1,22 ·e ^-21.600k = 1 | : e ^-21.600k 1,22 = e ^21.600k | ln

21.600k = ln 1,22 | : 21.600 k = ln 1,22 / 21.600 ≈ 9,206 · 10^-6

3. Schritt: k in eine der beiden Gleichungen einsetzen und diese Gleichung nach C auflösen.

k = 9,206 · 10^-6 einsetzen in die Gleichung C·e ^7200k = 100.000

C·e ^{7200
· 0,000009206} = 100.000

C·e ^0,0662836 = 100.000 | : e ^0,0662836

C = 100.000 ·e ^-0,0662836 ≈ 93.586,54