Aufgabe mit Musterlösung
von: Ansgar Schiffler
zurück zu 'Differentialrechnung'
1. Gegeben ist die Funktion y = f(x) = x³ - 4,8x² + 5x +1,2.

Bild 1: Der Graph der Funktion y = f(x) = x³ - 4,8x² + 5x +1,2 im Bereich -0,5 ≤ x ≤ 3,5
a.) Bestimmen Sie alle Nullstellen. Hinweis: N1(2|0) ist eine der drei Nullstellen.
b.) Bestimmen Sie die Koordinaten der Extrema (unterscheiden Sie nach Hoch- und Tiefpunkt) und des Wendepunktes. Hinweis: Geben Sie die Koordinaten auf fünf Stellen nach dem Komma gerundet an.
Kurzanleitung: Hoch- und Tiefpunkte bestimmen
Kurzanleitung: Wendepunkte bestimmen
c.) Bestimmen Sie die Gleichung der Tangenten, die den Graphen im Punkt P(0,4 | 2,496) berührt.
Musterlösung mit Erklärungen
a.) Bestimmen Sie alle Nullstellen. Hinweis: N1(2|0) ist eine der drei Nullstellen.
Erklärung: Nullstellen sind die Stellen, an denen der Funktionswert den Wert 0 hat. Es sind somit Schnitt- oder Berührpunkte des Graphen mit der x-Achse. Im folgenden Bild sind die drei Nullstellen des Graphen markiert!

Bild 2: Der Graph der Funktion mit markierten Nullstellen.
Wenn sich eine Nullstelle an der Stelle N1(x0|0) befindet, dann wird der Funktionsterm durch (x - x0) geteilt, in diesem Fall also durch (x - 2)
(x³ – 4,8x² + 5x + 1,2) : (x - 2) = x² – 2,8x – 0,6
– (x³ – 2,0x²)
__________
– 2,8x² + 5,0x
– (– 2,8x² + 5,6x)
________________
– 0,6x + 1,2
– (– 0,6x + 1,2 )
____________
0
Somit kann der Funktionsterm so dargestellt werden:
x³ - 4,8x² + 5x + 1,2 = (x – 2) · (x² – 2,8x – 0,6)
Um die Nullstellen zu bestimmen, wird dieser Term gleich null gesetzt.
(x – 2) · (x² – 2,8x – 0,6) = 0
Ein Produkt ist dann null, wenn mindestens einer der Faktoren null ist.
x – 2 = 0 | + 2 x = 2 (dieses Ergebnis war bereits vorgegeben)
x² – 2,8x – 0,6 = 0 Diese Gleichung lässt sich zum Beispiel mit Hilfe der pq-Formel nach x auflösen. Die Gleichung ist erfüllt für x1 = 3 und für x2 = -0,2.
Wir haben somit drei Nullstellen: N1(-0,2|0) ; N2(2|0) ; N3(3|0)
b.) Bestimmen Sie die Koordinaten der Extrema (unterscheiden Sie nach Hoch- und Tiefpunkt) und des Wendepunktes. Hinweis: Geben Sie die Koordinaten auf fünf Stellen nach dem Komma gerundet an.
Erklärung: Hoch- und Tiefpunkte (Extrema) haben eine besondere Eigenschaft: An diesen Stellen beträgt die Steigung der Tangenten an den Graphen null. Die Tangente verläuft also waagrecht.
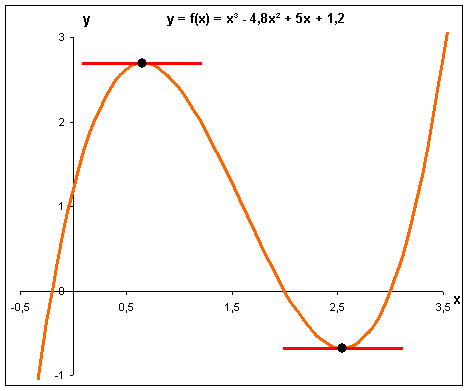
Bild 3: Der Graph der Funktion mit markierten Extrema. Es sind auch die jeweiligen Tangenten in Rot angedeutet. Es ist deutlich zu erkennen, dass die Tangenten waagrecht verlaufen.
Erklärung: Mit Hilfe der Ableitungsfunktion läßt sich die Tangentensteigung in jedem beliebigen Punkt ermitteln.
y = f(x) = x³ – 4,8x² + 5x +1,2
f '(x) = 3x² – 9,6x + 5
Wir möchten herausfinden, für welche x die Tangentensteigung null ist (waagrechte Tangente). Daher setzen wir die Ableitungsfunktion null und lösen die Gleichung nach x auf.
3x² – 9,6x + 5 = 0 | : 3
x² – 3,2x + 5/3 = 0
![]()
x1 = 1,6 + 0,94516 = 2,54516
x2 = 1,6 – 0,94516 = 0,65484
Hinweis: Dies sind nicht die exakten Ergebnisse. Die Ergebnisse sind auf fünf Stellen nach dem Komma gerundet angegeben. Wenn Sie mit diesen Werten weiterrechnen, sollten Sie nicht mit den gerundeten Werten rechnen, sondern diese Ergebnisse in Ihrem Taschenrechner speichern.
Erklärung: Um zu beurteilen, ob es sich bei einem Extremum um einen Hoch- oder einen Tiefpunkt handelt, muss der x-Wert in die zweite Ableitungsfunktion eingesetzt werden.
Die zweite Ableitungsfunktion liefert uns Informationen darüber, ob eine Rechts- oder eine Linkskurve vorliegt.
Wenn f ''(x) < 0 gilt, liegt eine Rechtskurve vor, die Steigung ist also abnehmend.
Wenn f ''(x) > 0 gilt, liegt eine Linkskurve vor, die Steigung ist also zunehmend.
Ein Hochpunkt (Maximum) liegt immer in einer Rechtskurve, die Steigung in der Umgebung des Hochpunktes ist also abnehmend.
Ein Tiefpunkt (Minimum) liegt immer in einer Linkskurve, die Steigung in der Umgebung des Tiefpunktes ist also zunehmend.
Also zusammenfassend kann gesagt werden:
f '(x0) = 0 und f ''(x0) < 0 : Im Punkt (x0|f(x0) befindet sich ein Hochpunkt.
f '(x0) = 0 und f ''(x0) > 0 : Im Punkt (x0|f(x0) befindet sich ein Tiefpunkt.
Hinweis: Falls f ''(x0) = 0 gilt, kann zunächst keine Aussage getroffen werden. In diesem Fall muss f '''(x0) berechnet werden. Wenn gilt : f '(x0) = 0 und f ''(x0) = 0 und f '''(x0) ≠ 0 gilt, liegt ein Sattelpunkt vor.
y = f(x) = x³ – 4,8x² + 5x + 1,2
f '(x) = 3x² – 9,6x + 5
f ''(x) = 6x – 9,6
f ''(2,54516) = 6 · 2,54516 - 9,6 = 5,67098 > 0 (also: Minimum)
f ''(0,65484) = 6 · 0,65484 - 9,6 = – 5,67098 < 0 (also: Maximum)
Die y-Koordinaten erhalten Sie, indem Sie die x-Werte in die Funktionsgleichung y = f(x) einsetzen:
f (2,54516) = 2,54516³ – 4,8 · 2,54516² + 5 · 2,54516 + 1,2 = –0,68069
f (0,65484) = 0,65484³ – 4,8 · 0,65484² + 5 · 0,65484 + 1,2 = 2,69669
Ergebnis:
H(0,65484 | 2,69669) T(2,54516|–0,68069)
Der erste Teil der Aufgabe (Bestimmung der Koordinaten der Extrema) ist gelöst. Im zweiten Teil der Aufgabe b bestimmen wir die Koordinaten des Wendepunktes.
Erklärung: Eine Wendepunkt hat die Eigenschaft, dass er sich direkt am Übergang von einer Rechts- zu einer Linkskurve (oder umgekehrt) befindet. Er befindet sich also weder in einer Rechts- noch in einer Linkskurve. Daher hat die zweite Ableitungsfunktion an der Stelle, an der sich ein Wendepunkt befindet, eine Nullstelle. Dies ist die notwendige Bedingung für einen Wendepunkt. Wenn zusätzlich gilt, dass die dritte Ableitungsfunktion an dieser Stelle ungleich null ist, liegt ein Wendepunkt vor.
f ''(x0) = 0 und f '''(x0) ≠ 0 : Im Punkt (x0|f(x0) befindet sich ein Wendepunkt.
Hinweis: Falls zusätzlich f '(x0) = 0 gilt, handelt es sich um einen Sattelpunkt.
f ''(x) = 6x – 9,6
6x – 9,6 = 0 | + 9,6 | : 6 x = 1,6
f '''(x) = 6 ≠ 0 (also: Wendepunkt)
Die y-Koordinate erhalten Sie, indem Sie den x-Werte in die Funktionsgleichung y = f(x) einsetzen:
f (1,6) = 1,6³ – 4,8 · 1,6² + 5 · 1,6+ 1,2 = 1,008
Ergebnis:
W(1,6 | 1,008)

Bild 4: Die Rechtskurve (abnehmende Steigung, 2. Ableitung negativ) ist Rot eingezeichnet. Die Linkskurve (zunehmende Steigung, 2. Ableitung positiv) ist Grün eingezeichnet.
Der Wendepunkt liegt genau am Übergang von Rechts- zu Linkskurve (weder ab- noch zunehmende Steigung, 2. Ableitung ist null).
c.) Bestimmen Sie die Gleichung der Tangenten, die den Graphen im Punkt P(0,4 | 2,496) berührt.
Hinweis: Diese Aufgabe gehört nicht zu klassischen Kurvendiskussion.
Erklärung: Die Tangentensteigung in einem beliebigen Punkt kann bestimmt werden, indem wir die x-Koordinate dieses Punktes in die erste Ableitungsfunktion einsetzen.
y = f(x) = x³ – 4,8x² + 5x + 1,2
f '(0,4) = 3·0,4² – 9,6 · 0,4 + 5 = 0,48 – 3,84 + 5 = 1,64
Also gilt: m = 1,64
Erklärung: Die allgemeine Geradengleichung lautet: y = m · x + b, wobei m die Steigung der Geraden ist und b der y-Achsenabschnitt (Schnittpunkt der Geraden mit der y-Achse). Wenn wir die Koordinaten eines beliebigen Punktes auf dieser Gerade in die Gleichung einsetzen, ist diese Gleichung erfüllt. Wir kennen einen Punkt der Geraden und zwar den Punkt P(0,4 | 2,496). Außerdem kennen wir die Steigung der Geraden: m = 1,64. Wir setzen also x = 0,4 ; y = 2,496 und m = 1,64 in die Gleichung ein und bestimmen b so, dass die Gleichung erfüllt ist.
y = m · x + b
2,496 = 1,64 · 0,4 + b
2,496 = 0,656 + b | – 0,656
b = 1,84
Ergebnis:
y = g(x) = 1,64x + 1,84
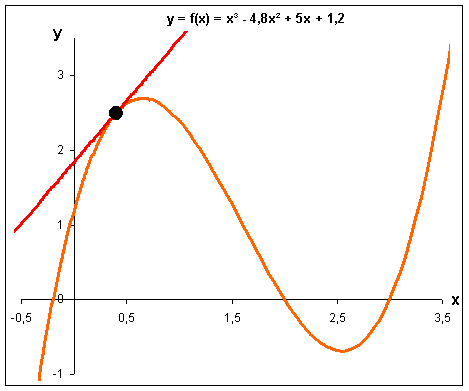
Bild 5: Die Tangente mit der Gleichung y = g(x) = 1,64x + 1,84 berührt den Graphen der Funktion f(x) im Punkt P( 0,4 | 2,496 ).
Zurück zur Aufgabenstellung (Seitenanfang)